第一节 天文学基础概念¶
1 位置与天球坐标系¶
1.1 天球概念与类型¶
我们已经知道,天体是宇宙间各类星体的总称。那么作为观测者,我们首先要对天体的位置进行合理描述。对于空间中天体的位置进行描述,必然涉及到给空间中的每个位置进行编号,这一编号的规则就是坐标系。因此,我们必须建立一个合适的坐标系。
建立一个合理的坐标系还意味着需要选择一个合理的参考点(原点),位置的测量将以这个原点为起点。这个原点可以是观测者本身的位置,还可以是地球中心、太阳中心或者银河系中心。通过选取一个位置作为原点,我们就能够很快建立坐标系,从而描述天体的位置、并对该位置开展观测。比如我们最熟悉的地理坐标系,原点就是赤道与本初子午线的交点,由此建立的坐标系就能够用经度和纬度进行确定。
我们经常用角度来描述位置。一个圆周360度,表示为360°;每一度分为60分,表示为60’;每一分由被分为60秒,记为60’’。
以前人们接受「地心说」,也就是说整个宇宙中心是地球,其它的天体比如太阳、月亮、星星等都是在嵌在「天」上绕着地球转。虽然这个学说早已经被证明是错误的,但是它对于人们理解天体位置有深刻的影响。之后的坐标系比如地平坐标系、赤道坐标系、黄道坐标系以及银道坐标系,都与这种假想的类似天球的概念有关。
对于天球,我们可以遵循类似的理解:当我们仰望天空的时候,太阳、月亮以及其它星星似乎都是分布在一个大的球面上,我们是没法分辨实际上哪些离我们更远、哪些离我们更近的,好像都是远远地固定在球面上;因此这些天体对于我们观测者而言,就好像是球面上的点(天体们)对于球心(这种情况下是观测者自己),无论我们在地球上的哪个位置都是这样。因此,我们可以将这些天体都看作是位于一个以观测者为中心,任意长度为半径的假想的球上,这个球就是天球。
对于天球的定义,有两点需要强调:
- 天球的中心是观测者(或者是地心/日心/银心)
- 天球的半径是任意的。也就是说,不论天体多遥远,天球上都有它的投影。
因此,根据天球中心的不同,可以分为观测者天球、地心天球和日心天球等等。由于在较大尺度的空间范围内地球的半径可以忽略,因此在大部分描述太阳系以外天体的视位置和视运动的情况下,地心天球和地面观测者天球可以看作是一致的。
设定天球的优势就在于,我们不必知道天体与我们的真实距离,只需要将天体的视位置(天体在天球上的投影)表示在天球上,这样我们表述其视运动也比较容易。
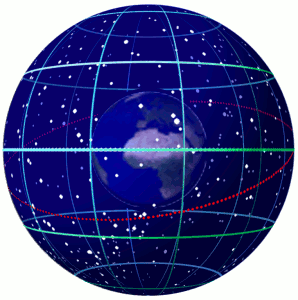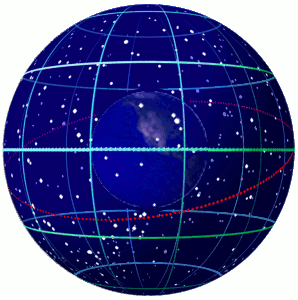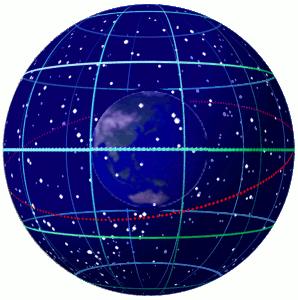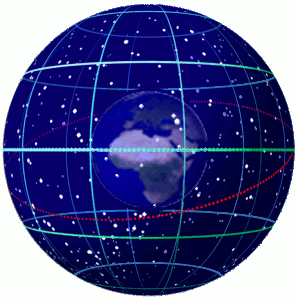
地球在一个半径相对细小,以地球为基础的天球中旋转的动画。图中还可见黄道(红)和天球坐标系统上的赤经、赤纬(绿)。
1.2 天球基本圈与基本点¶
在天球上作一些假象的点与圈,有助于我们通过点线关系确定天球上的视位置、并且研究天球上的视运动。这些基本圈和基本点在天文摄影中具有重要作用。
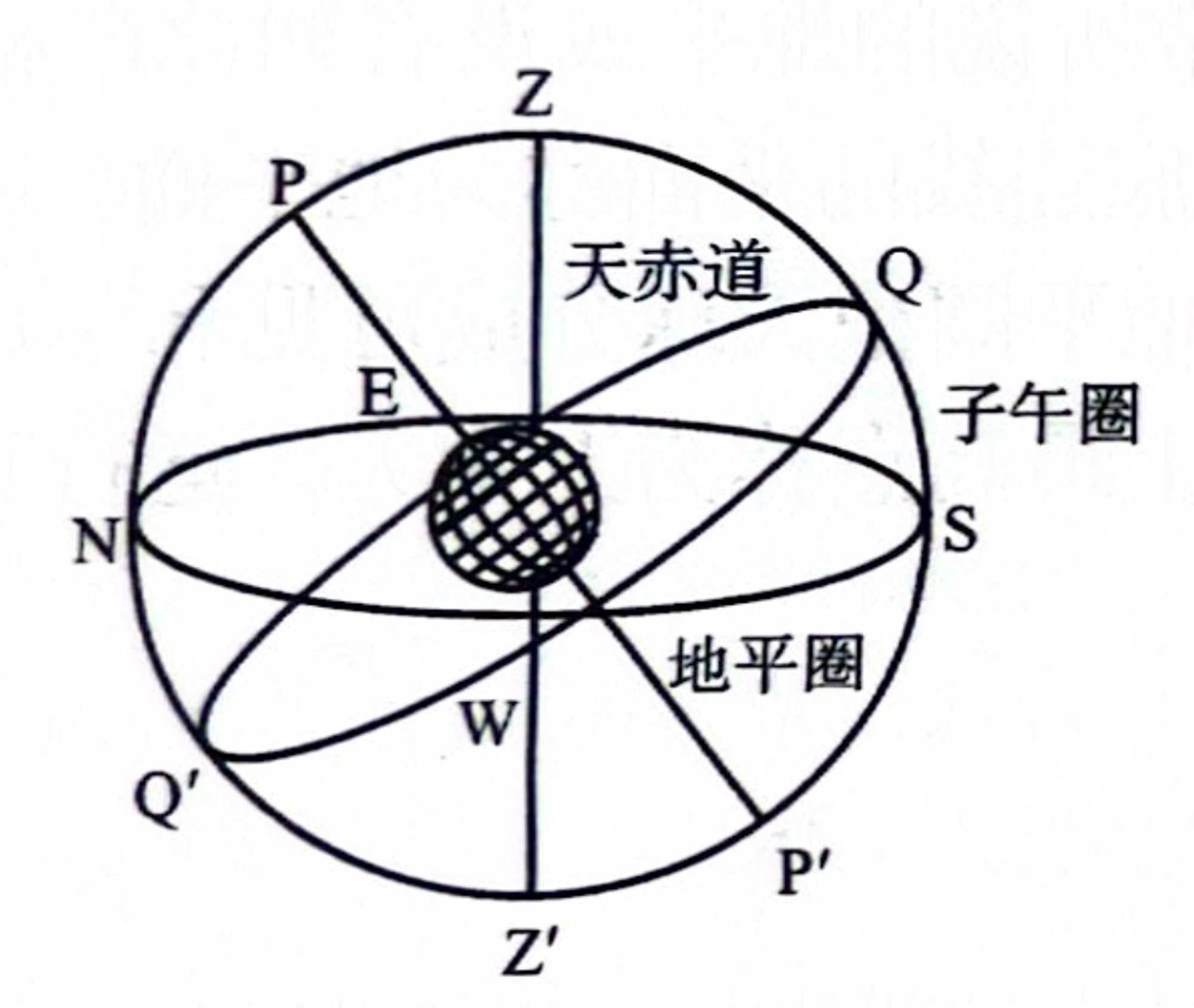
- 天顶(Z):沿观测者头顶所指的方向作直线向上无限延伸,与天球相交的一点。
- 天底(Z’):沿观测者脚底方向(向地平以下无限延伸)与天球相交的另一点。
- 地平圈(NWSE):通过地心并且垂直于观察者所在地点的垂线的平面与天球相交的大圆。或者表述为,通过天球中心垂直于天顶与天底连线的平面(地平面)和天球相交的大圆。
- 上中天:天体每日视运动运行到距离地平圈以上的最高点。
- 下中天:天体每日视运动运行到距离地平圈最低点。
- 天轴:地轴无限延伸。
- 天极(P与P’):天轴与天球相交的点。有北天极和南天极。
- 北天极(P):与地球北极对应的天极。小熊座𝛼星(中名“勾陈一”)在北天极附近约1°处,称为北极星
- 南天极(P’):与地球南极对应的天极。南天极及附近没有亮星,因此没有“南极星”。
- 天赤道:与北天极和南天极距离相等,且垂直于天轴的大圆。或者表述为,地球赤道面无限扩展与天球相交形成的圆。将天球分割成北半球和南半球。
- 北点(N):通过天顶和天底、北天极和南天极的大圈与地平圈相交的两点中,靠近北天极的一点。
- 南点(S):通过天顶和天底、北天极和南天极的大圈与地平圈相交的两点中,靠近南天极的一点。
- 东点(E):自北点顺时针旋转90°的那一点。
- 西点(W):与东点相距180°的那一点。
- 子午圈(PZSP’Z’N):通过天顶和北天极同时又经过北点和南点的大圈。
天顶(Z)、天底(Z’)、天极(P与P’)、天赤道、地平圈(NWSE)、四方点(NWSE四个点)。图源简明天文学第四版,徐明等编著。
- 黄道:通过天球中心作一与地球公转轨道面叠加的无限平面,这个平面为黄道面;黄道面和天球相交的大圆为黄道。也可表述为,地球绕日公转轨道面任意扩展与天球相交的大圆。可以看出,黄道即为地球公转轨道在天球上的投影。K为北黄极、K‘为南黄极。
- 太阳的周年视运动在天球上的轨迹就是黄道。
- 行星在天球上的视运动轨迹就在黄道附近。(因为太阳系内主要行星的轨道平面都非常接近黄道面。)
- 银道:在天球上沿着银河中心画出的大圆。是银河系平均平面(银道面)与天球相交的大圆,与天赤道形成约63.5°夹角。
- 黄赤交角:黄道平面与天赤道平面形成的约23°26’的夹角。这一交角的存在使得黄道和天赤道有两个交点,即 春分点 和 秋分点 。
- 春分点:在北半球看来,春分点是升交点,即太阳在黄道上运行过该点后便升到天赤道平面之上;
- 秋分点:在北半球看来,秋分点是降交点,即太阳在黄道上运行过该点后便降到天赤道平面之下。
黄道、黄极、二分二至点。图源简明天文学第四版,徐明等编著。
1.3 天球坐标系¶
天球坐标:由天球上的纬度和经度所组成的坐标。
天球坐标系的一般模式主要包括:
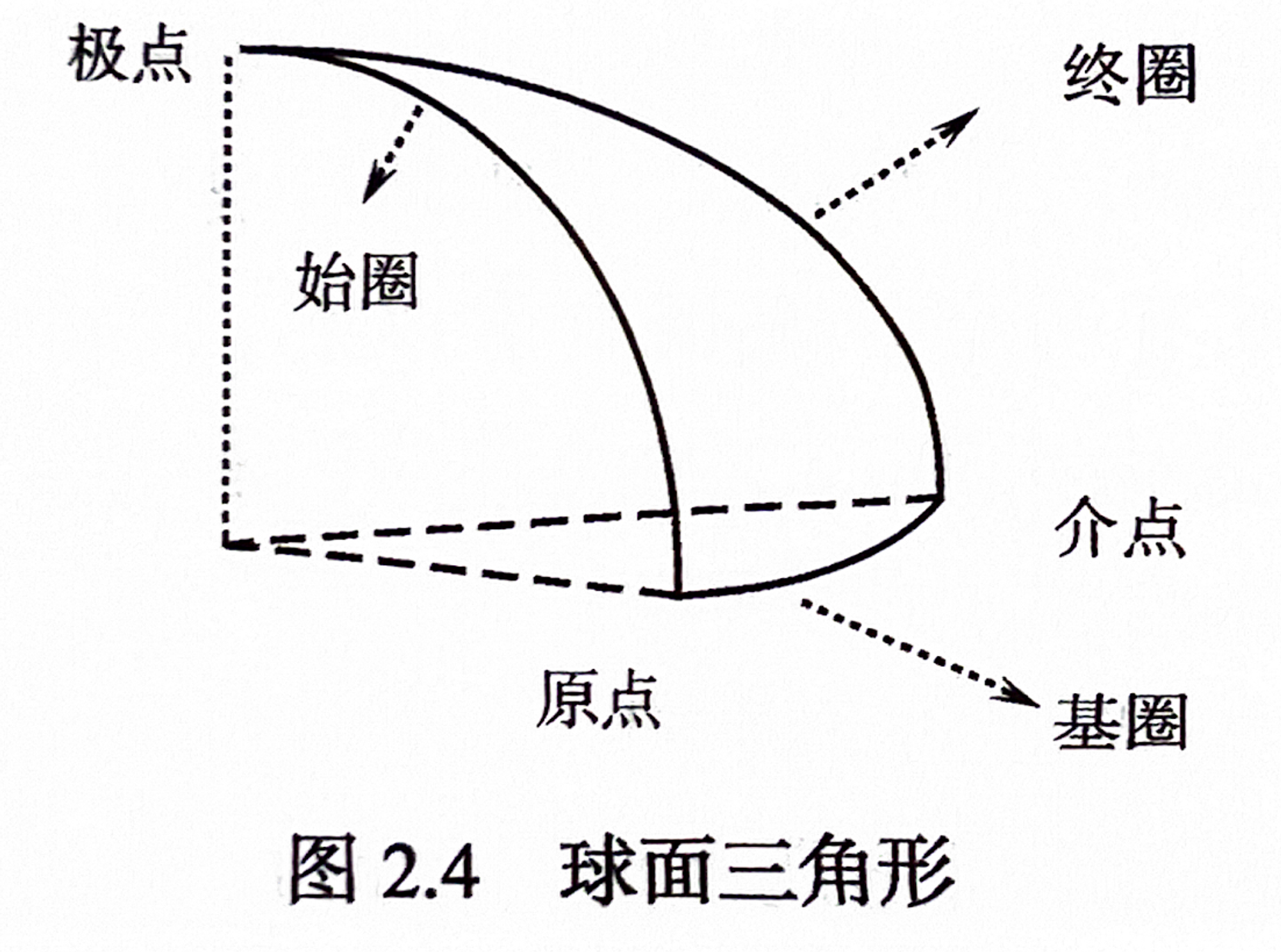
- 基圈:球面坐标的「纬度」起算圈,代表坐标系的「横轴」
- 始圈:球面坐标的「经度」起算圈,代表坐标系的「纵轴」
- 终圈:球面坐标的「经度」终止圈
- 极点:始圈与终圈相交的轴与两者的交点。「纬度」为90°。
- 原点:始圈与基圈的交点
- 介点:终圈与基圈的交点
通过这样的球面三角形模式,可以利用一定的经度和纬度确定天球上任意一点的位置。
球面三角形模式。图源简明天文学第四版,徐明等编著。
1.3.1 地平坐标系¶
- 由高度(h)和方位(A)组成
- 非常直观表示观察者所见的天体在天球上的位置。
- 坐标系构成:
- 基圈:地平圈
- 原点:南点(S)
- 始圈:午圈
- 纬度表示:高度(h),天体与地平圈的角距离,也即天体的仰角。范围为-90°到90°;天体在地平面之上为正,此时天体可见;在地平面之下为负,此时不可见。高度的余角为天顶距(\(Z_0\))。
- 经度表示:方位(A),天体相对于午圈的角距离。范围为0°到360°;从午圈经过的南点开始,沿着地平圈(基圈)按顺时针方向(向西)度量。
- 天体通过子午圈且高度最大时叫做上中天;通过子午圈且高度最小时为下中天。(观测者位于地球两极时不考虑两者)
- 应用场景:
- 航海、航空、大地测量
- 描述一天中太阳高度的变化及一年中正午太阳高度的变化
- 观测流星、彗星、人造卫星等天体位置
- 经纬仪(地平式支架)用的就是这个坐标系。
- 天体坐标随着观测者所在地点与观测时间改变而改变。
地平坐标系。图源基础天文学教程,邵华木等编著。
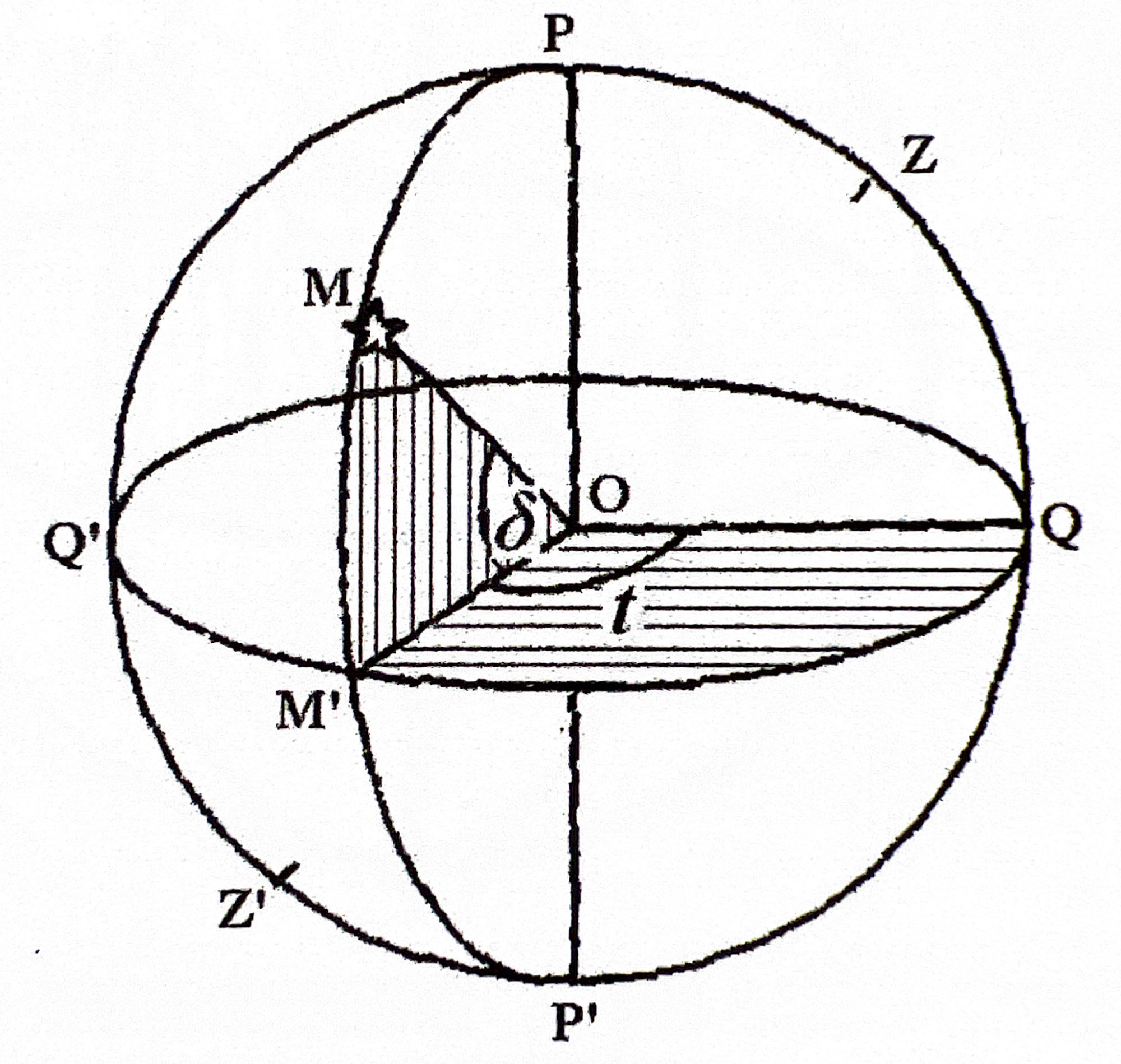
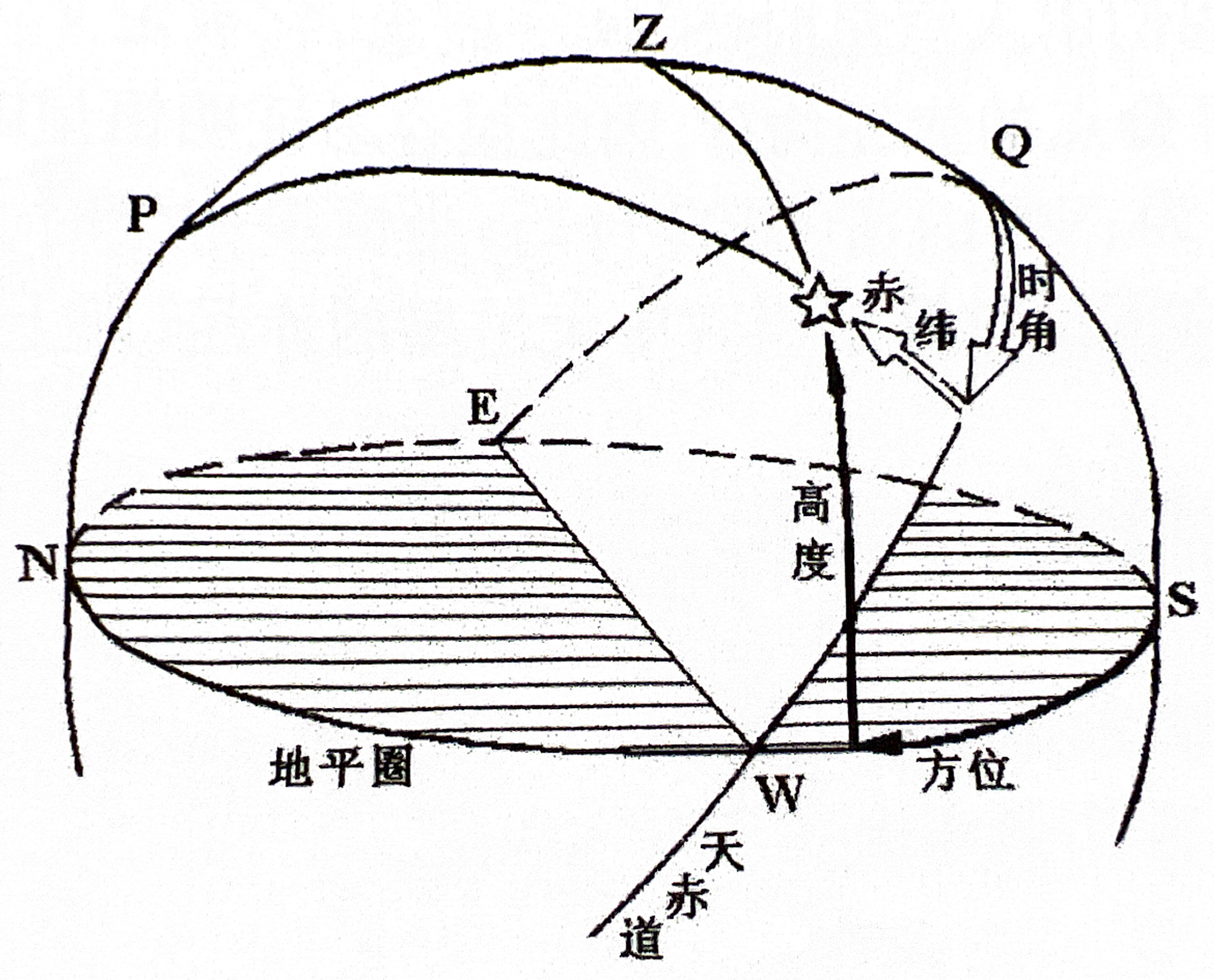
1.3.2 第一赤道坐标系(时角坐标系)¶
- 由赤纬(\(\delta\))和时角(\(t\))组成
- 用于时间的度量
- 坐标系构成:
- 基圈:天赤道
- 原点:上点(Q)
- 始圈:午圈
- 纬度表示:赤纬(\(\delta\)),天体相对于天赤道的角距离。范围为-90°到90°,余角称为极距。
- 经度表示:时角(\(t\)),天体相对于午圈的角距离。度量方式与地平坐标系的方位角类似,只不过换成了时间单位,范围为\(0^h\)~\(24^h\),15°为\(1^h\),15’为\(1^m\),15’’为\(1^s\)。
- 应用场景:天文学中规定春分点的时角为恒星时。春分点上中天时恒星时为\(0^h\),随着地球的自转,春分点在天球上不断向西移动,时角不断增大,意味着时间不断流逝。因此可以用于时间度量。
- 天体坐标随着观测者所在地点与观测时间改变而改变。
第一赤道坐标系。图源基础天文学教程,邵华木等编著。
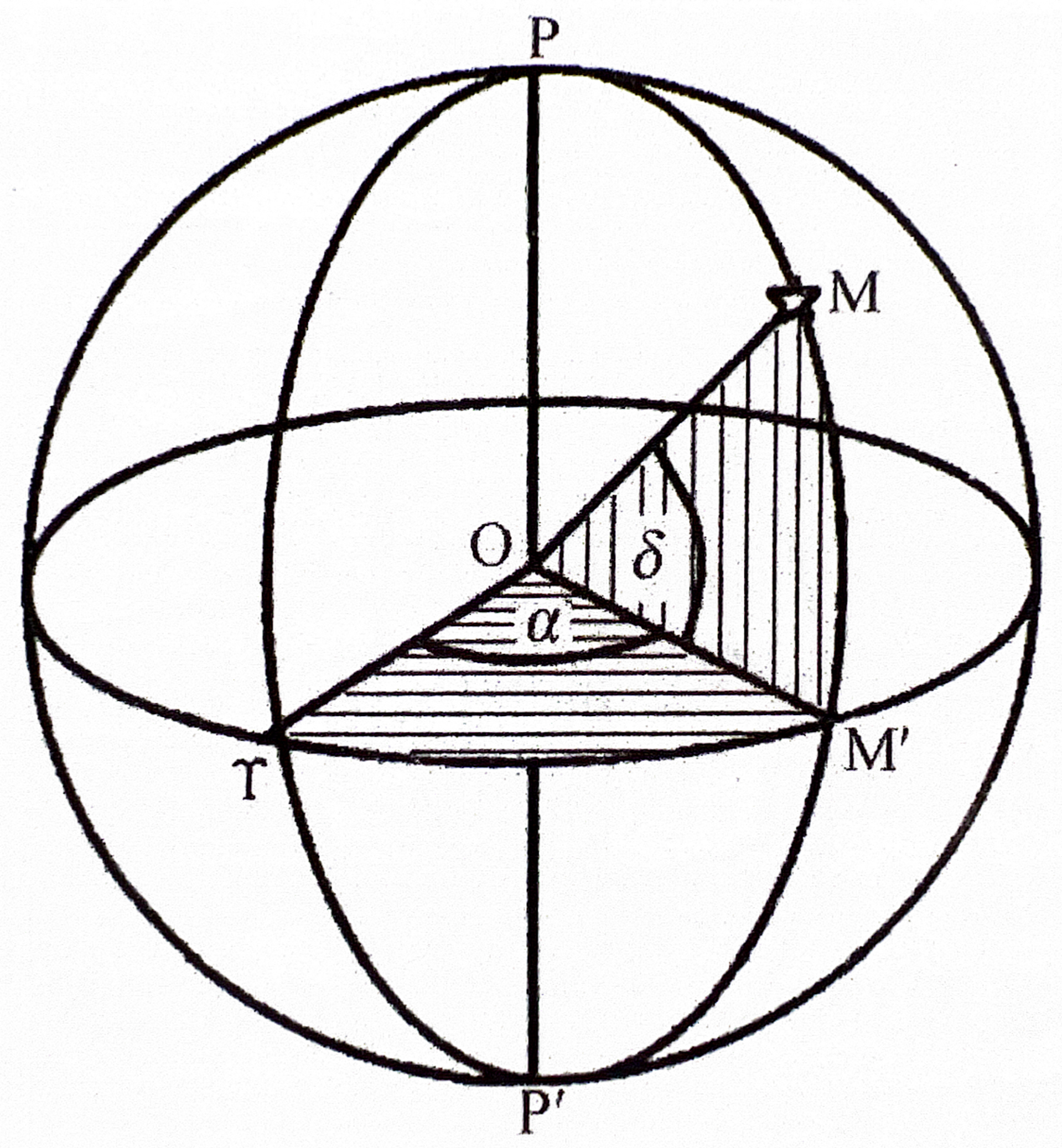
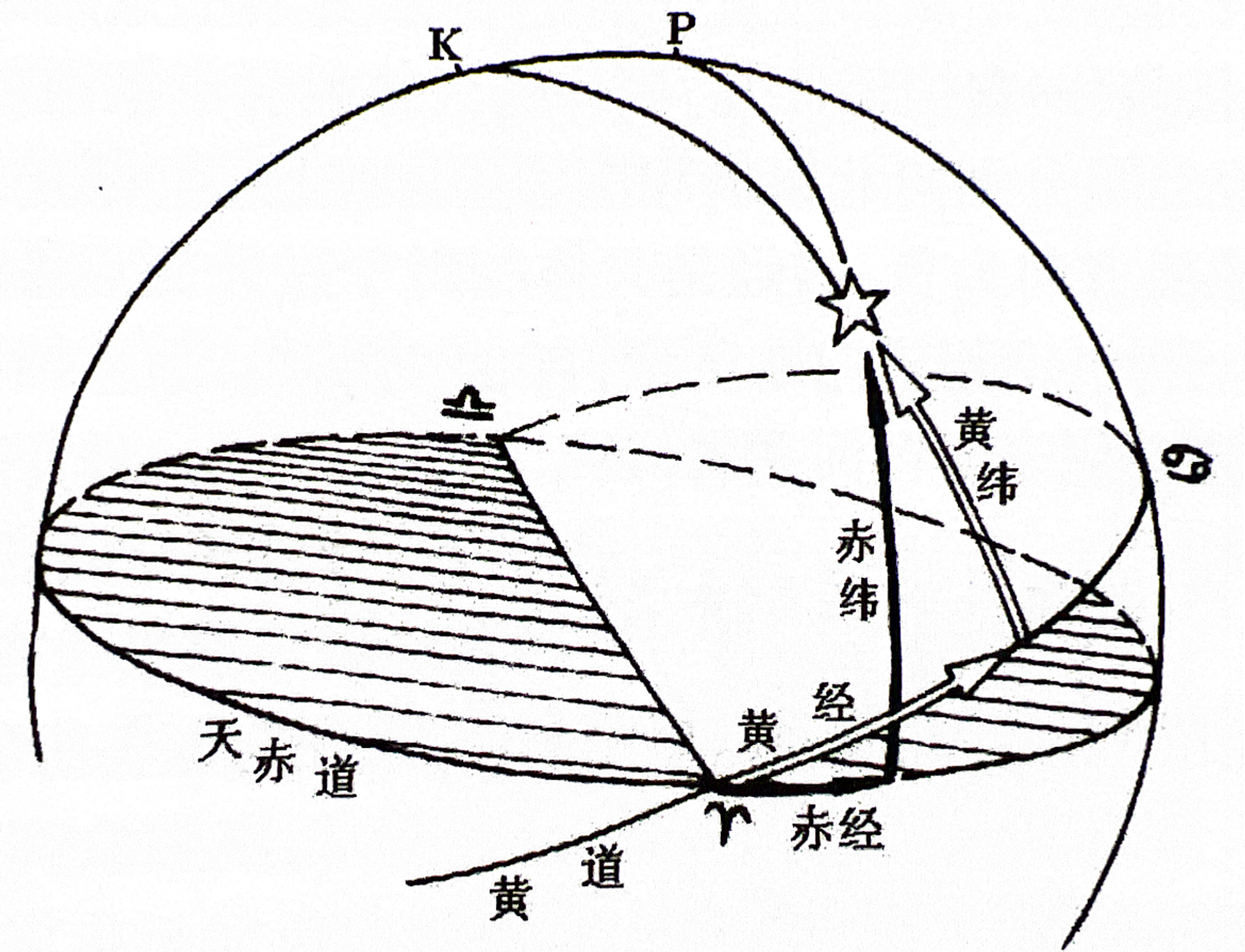
1.3.3 第二赤道坐标系¶
- 由赤纬(\(\delta\))和赤经(\(\alpha\))组成
- 用于 编制星表,赤道仪常用该坐标系进行GOTO 。
- 坐标系构成:
- 基圈:天赤道
- 原点:春分点(黄道与天赤道相交的升交点)
- 始圈:春分圈(通过春分点的时圈)
- 纬度表示:赤纬(\(\delta\)),与第一赤道坐标系相同, 天体相对于天赤道的角距离 。范围为-90°到90°。
- 经度表示:赤经(\(\alpha\)), 天体所在时圈相对于春分点的方向和角距离 。范围同样用时间表示,\(0^h\)~\(24^h\),从春分点开始向东度量。
- 应用场景:
- 编制星表,注明天体(例如恒星、星系、星团)在天球上的固定位置
- 目前天文摄影(尤其是深空摄影)中常用的赤道仪(赤道式支架)就是按照第二赤道坐标系制作的。将赤道仪的极轴对准北天极,此时赤道仪的赤经赤纬与天球上赤经赤纬相对应,通过星表中天体的赤经赤纬坐标,就能够指向天球上任意位置。
- 在一定时间内(几百年或上千年)天赤道和春分圈相对空间位置变化很小,在较短时间内总是适用的。但是由于地轴进动/岁差(地轴是摆动的),天赤道的空间位置实际上也是不断摆动的,在较长的时间内,需要更新星表以适应天体赤经赤纬的变化。因此 星表也需要注明编制的年份 。
第二赤道坐标系。图源基础天文学教程,邵华木等编著。
岁差
岁差一般指地球自转轴缓慢且均匀地变化。岁差的具体影响分为 赤道岁差 和 黄道岁差 。 赤道岁差 表现为春分点在黄道上每年西退50’’.29,周期为25722年。

岁差。图源:剑桥天文爱好者指南,Michael E. Bakich著,李元等译。
1.3.4 黄道坐标系¶
- 由黄纬(\(\beta\))和黄经(\(\lambda\))组成
- 用于描述太阳系成员的视位置和视运动
- 坐标系构成:
- 基圈:黄道
- 原点:春分点
- 始圈:过春分点的黄经圈(通过两个黄极的大圆)
- 纬度表示:黄纬(\(\beta\)),天体与黄道之间的角距离,范围为-90°到90°。
- 经度表示:黄经(\(\lambda\)),天体对于春分点所在的黄经圈的角距离,以春分点为原点沿着黄道向东度量。
- 太阳总在黄道上,太阳的黄纬始终为0°;太阳的黄经每日增加59’。月球以及太阳系其他行星的黄纬不大(几乎都在一个平面上)。行星有时顺行有时逆行,因此行星黄纬不一定总是与日俱增。
黄道坐标系。图源基础天文学教程,邵华木等编著。
1.3.5 银道坐标系¶
由银纬和银经组成。天文爱好者观测时不常用,主要用于星系天文学,以及对银河系的研究,这里不做过多解释。
1.3.6 各类天球坐标系的比较和联系¶
这里不对角度关系作过多解释,只放了教材上的一些图以便理解。
地平坐标系与第一赤道坐标系之间的关系。图源基础天文学教程,邵华木等编著。
第二赤道坐标系与黄道坐标系之间的关系。图源基础天文学教程,邵华木等编著。
第一赤道坐标系与第二赤道坐标系之间的关系。图源基础天文学教程,邵华木等编著。
天球坐标系比较表格。图源简明天文学第四版,徐明等编著。
2 天体的视运动和四季星空¶
2.1 天体的周日视运动¶
- 概念:是指所有天体在天球上以一天为周期的自东向西的运动。
- 实质:地球自西向东的自转。
- 运动特点:
- 转轴:天轴。因此会发现星星似乎都是绕着北极星转的,实际就是绕着北天极对应的天轴转的。
- 方向:自东向西。
- 周期:恒星周日运动的周期就是恒星日,代表地球自转的真正周期;太阳周日运动周期为太阳日,代表地球昼夜更替的周期。由于地球自转的同时还绕太阳公转,太阳日比恒星日长3’56’’,这也造成全年中星座每天提前一点升起。
- 角速度:与地球自转角速度相同,每小时15°。
- 实际在天文摄影中的应用:
- 星轨 。将相机固定,每隔一段时间拍照,最大值叠加后即可得到星星运动的轨迹,其实就是天体的周日视运动。因此 照片上的星轨描绘了一个个天纬线圈 。
笔者之前拍的星轨图。
2.2 太阳的周年视运动¶
- 概念:地球公转引起的太阳在恒星背景上的运动。表现为四季星空的更迭。
- 实质:地球自西向东绕太阳公转。
- 运动特点:
- 转轴:北黄极和南黄极的连线。
- 方向:自西向东。
- 周期:在地心天球上,日心连续两次通过黄道上的同一恒星的时间间隔,为恒星年;连续两次通过春分点,为回归年。
- 角速度:对应地球公转角速度。
- 应用:
- 节气等
- 导致一年四季所见到的星空不同:我们能够在一年中依次看到与太阳视位置所在星座/星区的赤经相差180°附近星区的星座/星区。
2.3 四季星空¶
- 1922年国际天文学会确定全天共88个星座;
- 天赤道以北的有29个、天赤道以南的46个、横跨黄道两侧的有13个。注意蛇夫座也属于黄道星座。在这里不讨论玄乎的所谓占星学的「星座」。关于「黄道十二宫」和黄道星座,可以见这一篇北京天文馆的科普文章,总结的很好。
- 结合之前对天体视运动的介绍,星空的变化包括两方面:
- 地球 自转 导致的 周日变化 :同一天星空因时刻而不同,自东向西。
- 地球 公转 导致的太阳视运动所造成的 周年变化 ,同一时刻不同季节星空不同。
3 星等系统¶
星等是描述天体亮度和光度一个非常重要的概念,有助于帮助我们进行天文摄影时估计并比较天体的亮度。
3.1 天体亮度与视星等¶
- 天体亮度:正常视力的人在地球上用肉眼所见到天体的明亮程度。
- 视星等:表示天体亮度等级,用\(m\)表示。
因此可以发现,视星等反映的仅仅是天体在天空中看起来的亮度。因为对于视星等而言,影响因素包括:
- 天体本身的发光能力
- 天体与地球的距离
- 天体辐射穿过星际空间的环境状况(例如星际尘埃遮挡等)
- 大气层对天体发出不同波段光的散射作用
- 人眼对天体发出不同波段光的响应等等。
古希腊天文学家喜帕恰斯将恒星亮度分为6个星等,最亮为1等、最暗为6等。随着观测技术的进步,人们发现了更多更暗的星,随后将视星等系统向6等以上1等以下(包括负值)拓展,星等可以为负数,并且保留了星等数越大越暗的规律。后来人们发现1等星的亮度大约是6等星的100倍,再加上人们当时认为人眼是以对数尺度感受亮度的差别,因此规定星等相差1等,亮度相差\(\sqrt[5]{100}=2.5118865\)倍。这个比例称为 普格逊比率 。
例如,A天体亮度为\(E_1\)、目视星等为\(m_1\),B天体亮度为\(E_2\)、目视星等为\(m_2\),则B与A亮度之比为:
由于\(lg2.512 \approx 0.4\),两边取对数得:
即:
如果取0等星\(m_1=0\)的亮度\(E_1=1\),则视星等的大小(\(m_2\))可以由普森公式计算:
其中\(m_2\)为目标天体目视星等,\(E_2\)为目标天体亮度,可以精确测定。
关于人眼感受亮度差别的规律
实际上,虽然以前的人认为人眼是对数探测器(见韦伯-费希纳定律),但是后续发现应该是幂定律。即感受强度\(S\)与刺激强度\(I\)之间的关系可以用幂函数表示:
其中\(k\)和\(n\)是常数。
对于视觉感知,斯蒂文斯幂律通常比韦伯-费希纳定律更为准确。因此目视星等用于定量比较不够严谨,可以用于定性大致比较亮度。
比如全天最亮的恒星(除了太阳)天狼星为-1.45等,织女星为0等,金星最亮时为-4.22等,月亮满月时亮度为-12.73等,太阳亮度为-26.74等。
天体的目视星等。图源简明天文学第四版,徐明等编著。
夜晚天空的亮度。用每平方弧秒的视星等衡量。(表格来源:剑桥天文爱好者指南)
| 月周期 | 蓝色滤光片 | 可见光滤光片 | 红色滤光片 |
|---|---|---|---|
| 0(新月) | 22.7 | 21.8 | 20.9 |
| 3 | 22.4 | 21.7 | 20.8 |
| 7 | 21.6 | 21.4 | 20.6 |
| 10 | 20.7 | 20.7 | 20.3 |
| 14(满月) | 19.5 | 20.0 | 19.9 |
3.2 天体光度和绝对星等¶
天体亮度和目视星等仅仅表征的是天体看起来有多亮,而如果需要直接比较天体实际的亮度,则需要考虑目视亮度与其距离的平方呈反比,将恒星假想在同一距离外进行比较。当距离相同时,目视亮度越高,天体本身的发光能力就越强。
天体本身的发光强度用 光度 描述,使用 绝对星等 表示天体的光度等级。也就是说,在标准距离处的天体的发光本领称为光度,其星等称为绝对星等。
标准距离
天文学上把这个标准距离定为10个秒差距(10pc),相当于0’’.1周年视差的距离,合32.6光年。
秒差距是 一个天文单位所张角度为1角秒所对应的距离 。主要用于太阳系以外的天体测量。英文parsec,缩写为pc,pc是parallax(视差)和second(秒)两词缩写的结合。天体的周年视差为1角秒,其距离即为1秒差距(1pc);天体的周年视差与其距离呈反比。还有千秒差距(kpc)以及百万秒差距(Mpc)。
设某天体在10pc处绝对星等为\(M\),亮度(此处代表光度)为\(E_0\);与观测者距离为\(d\)(此处单位为pc),亮度为\(E\),视星等为\(m\),由前可得:
天体亮度与距离呈反比:
因此有:
整理得:
因此,如果已知某天体的距离\(d\)以及视星等\(m\),可以求出绝对星等\(M\)。
彗星和小行星的绝对星等
对于彗星和小行星,使用的是一套不同的「绝对星等」系统。此时,绝对星等是一个假设的观测值站在太阳上,而一个彗星或小行星处于一个天文单位的距离上,观测者看到的它的视星等。
如果按绝对星等计算,太阳的绝对星等为4.75,仅仅是茫茫恒星世界的普通一员,还有无数恒星离我们很远,但是其光度比太阳高100万倍。
参考资料¶
- 《简明天文学第四版》,徐明等编著
- 《基础天文学教程》,邵华木等编著
- 《剑桥天文爱好者指南》,Michael E. Bakich著,李元等译
- 北京天文馆科普文章